我們先來(lái)看誤差和不確定的概念：

測(cè)量不確定度：

 

國(guó)家計(jì)量技術(shù)規(guī)范：JJF1059《測(cè)量不確定度評(píng)定與表示》中定義是：“表征合理地賦予被測(cè)量之值的分散性，與測(cè)量結(jié)果相聯(lián)系的參數(shù)”

 

附帶三個(gè)注釋

 

注1：此參數(shù)可以是諸如標(biāo)準(zhǔn)偏差，或其倍數(shù)，或說(shuō)明了置信水平的區(qū)間的半寬度。

 

注2：測(cè)量不確定度由多個(gè)分量組成。其中一些分量可用測(cè)量列結(jié)果的統(tǒng)計(jì)分析估算，并用實(shí)驗(yàn)標(biāo)準(zhǔn)偏差表征。另一些分量則可用基于經(jīng)驗(yàn)或其它信息的假定概率分布估算，也可用標(biāo)準(zhǔn)偏差表征。

 

注3：測(cè)量結(jié)果應(yīng)理解為被測(cè)量之值的最佳估計(jì)，而所有的不確定度分量均貢獻(xiàn)給了分散性，包括那些由系統(tǒng)效應(yīng)引起的（如與修正值和參考標(biāo)準(zhǔn)有關(guān)的）分量。

 

測(cè)量誤差（簡(jiǎn)稱為誤差）的定義為：“測(cè)量結(jié)果減去被測(cè)量的真值”誤差應(yīng)該是一個(gè)確定的值，是客觀存在的測(cè)量結(jié)果與真值之間差。但由于真值往往不知道，故誤差無(wú)法準(zhǔn)確得到。

 

根本區(qū)別：

 

量不確定度是表征合理地賦予“被測(cè)量之值”的分散性，因此，不確定度表示一個(gè)區(qū)間，即“被測(cè)量之值”可能分布區(qū)間。這是測(cè)量不確定度與誤差的最根本的區(qū)別。

 

誤差的概念早已出現(xiàn)，但在用傳統(tǒng)方法對(duì)測(cè)量結(jié)果進(jìn)行誤差評(píng)定時(shí)，還存在一些問(wèn)題。

 

把被測(cè)量在觀測(cè)時(shí)所具有的大小稱為真值，只是一個(gè)理想的概念，只有通過(guò)完善的測(cè)量才有可能得到真值。但是任何測(cè)量都會(huì)存在缺陷，因而真正完善的測(cè)量是不存在的，也就是說(shuō)，嚴(yán)格意義上的真值是無(wú)法得到的。由于真值無(wú)法知道，在實(shí)際上誤差的概念只能用于已知約定真值的情況下。

 

根據(jù)誤差的定義，誤差是一個(gè)差值，它是測(cè)量結(jié)果與真值或約定真值之差。在數(shù)軸上它表示為一個(gè)點(diǎn)，而不是一個(gè)區(qū)間或范圍。既然是一個(gè)差值，就應(yīng)該是一個(gè)具有符號(hào)的量值。既不應(yīng)當(dāng)，也不可以“±”號(hào)的形式表示。

 

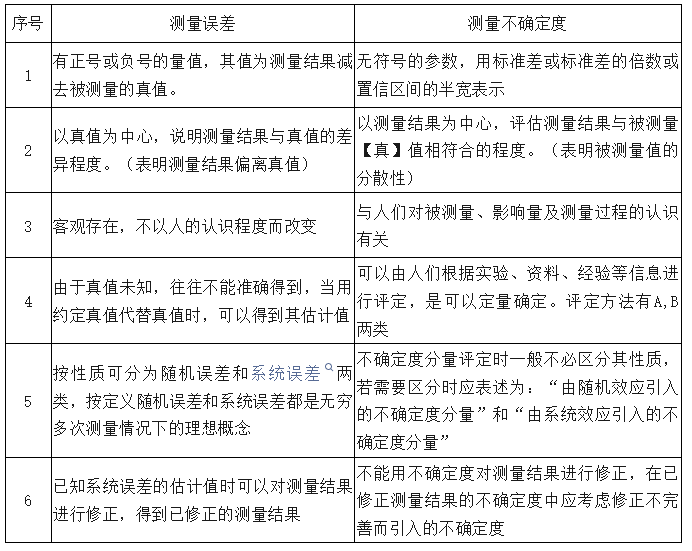
我們具體以表格的形式來(lái)說(shuō)明不確定度和誤差的區(qū)別：